Ми зібрали ключові новини з фізики за лютий 2021 року та з’ясували, що здійснювати відкриття на ВАК можна і з відпустки, а фізики з ЦЕРНу полюбляють розвінчувати магічність та обмежувати час народження античастинок. Вчені взагалі люблять обмеження, а тому вивели формулу для верхньої межі швидкості квантових операцій та обмежили зарядовий радіус ізотопа гелію з п’ятикратною точністю. Втім, обмеження можна і обходити, а тому цього місяця ми маємо аж дві перемоги квантового комп’ютера над класичним - на математичному та фізичному полях бою.
Великий адронний колайдер з відпустки розповів про розпад бозона Хіггса
Фізики побачили рідкісний розпад бозона Хіггса одразу на три частинки і сподіваються побачити у ньому механізм порушення симетрії зарядової та дзеркальної парності.
Якщо ми зараз відмотаємо наш годинник десь на 10⁻¹⁰секунди після народження Всесвіту, то ми маємо побачити приблизно те саме, що побачили на детекторі Гаргамель у 1973 році. І там, і там відбулося об'єднання електромагнітної та слабкої взаємодій, а за останнє вчені потім отримали Нобелівську премію у 1979 році. Втім, одні з учасників цієї взаємодії — W- і Z- бозони, виявилися майже у 80 разів «важчими» за протон, тож щось мало їхню з фотонами симетрію порушити. Так у 2013 відзначили Нобелівською Пітера Хіггса за передбачення дуже красивого механізму її порушення — хіггсівського. Відлуння цього механізму ми вперше побачили на Великому адронному колайдері ще у 2012 році та остаточно склали «пазл» з елементарних частинок Стандартної моделі. Це була одна із найголовніших наукових подій, але і після того ВАК не припинив роботу, бозон Хіггса не втратив уваги фізиків, а відповіді на всі питання Стандартної моделі не були знайдені.
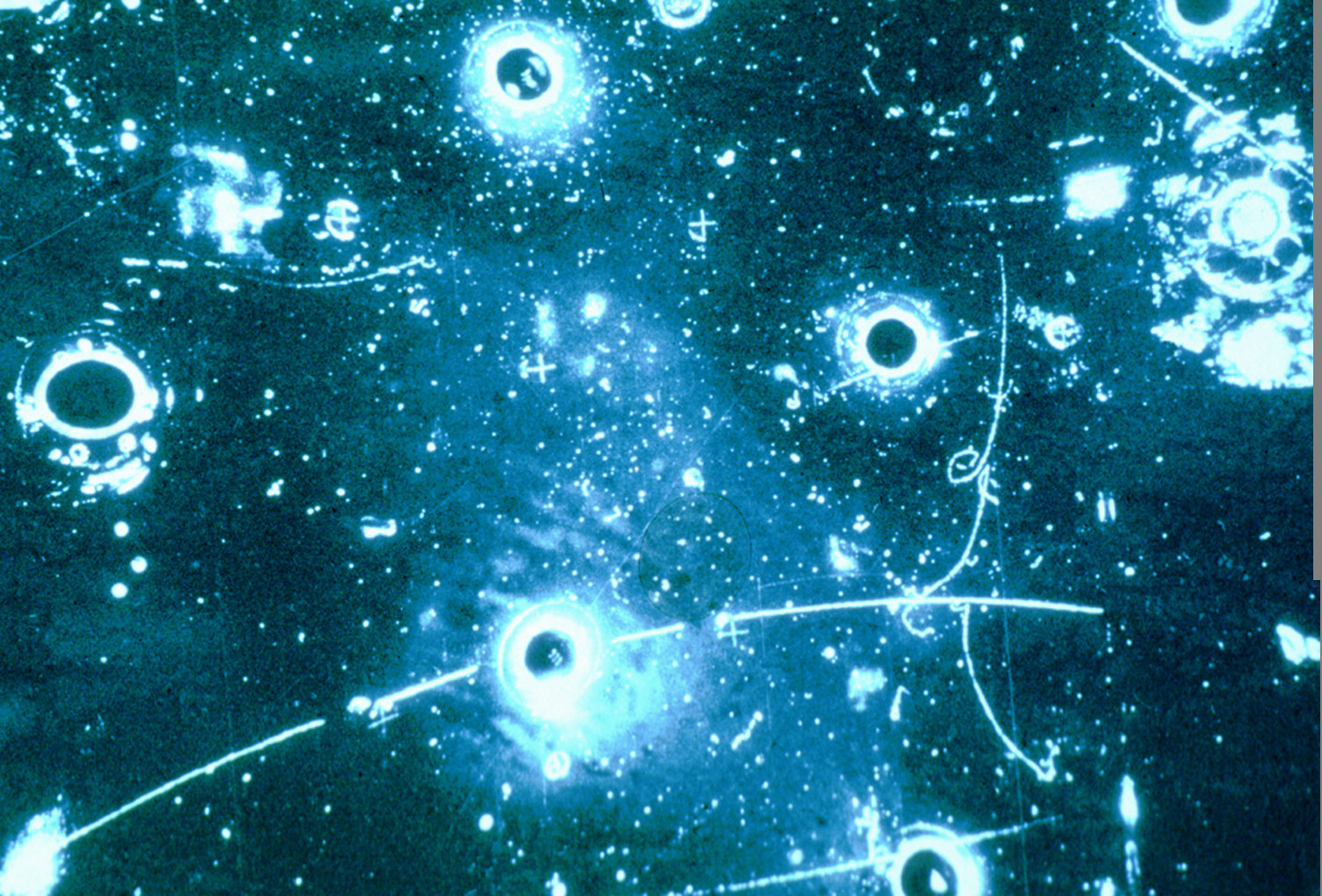
Треки частинок, які підтвердили існування нейтрального струму, а з ним і W- та Z-бозони, що стало кроком до підтвердження об’єднання електромагнітної та слабкої взаємодій у єдину електрослабку. CERN / Wikimedia Commons
Тепер вчені «колекціонують» розпади частинки. Колекціонують і з острахом (або ентузіазмом) очікують, що одного разу знайдуть такий розпад бозона Хіггса, якого теорія не передбачувала. Це вкаже на так звану Нову фізику — фізику за межами Стандартної моделі. Але поки цього не сталося можна видихнути і збирати рідкісні розпади бозона, ймовірність яких хоч і передбачається Стандартною моделлю, але вона істотно нижча тих, що ми можемо постійно бачити. Цього разу фізики вперше впіймали бозон Хіггса за розпадом одразу на три частинки — пару лептонів і фотон. У цьому їм допоміг Великий адронний колайдер, а точніше дані з другого сезону його роботи перед тим як він пішов на вимушену відпустку.
Що нам від того, що бозон так розпався? Окрім того, що такий тричастинний розпад ми хоч і передбачали, але досі не бачили, він може вказати на порушення СР-симетрії. Фізики говорять, що для того, щоб ми з вами були зараз тут, процес перетворення частинки на античастинку та дзеркальна симетрія процесів мали порушитися. Тобто якимось чином звичайна матерія мала встояти перед антиматерією та уникнути анігіляції, чим народила нам наш зарядово асиметричний Всесвіт. А оскільки у такому тричастинному розпаді обов’язково має брати участь якась проміжна частинка (Z-бозон або фотон), то вона і могла б своєю енергією порушити цю симетрію у бозоні Хіггса, що фізики і прагнуть дослідити.
Фізики засумнівалися у «магічності» ядер з 32 нейтронами
Вчені з експерименту «Ізольда» розвінчали восьмирічне переконання у тому, що число 32 також варто називати магічним. Для цього вони досліджували ізотопи калію, а у майбутньому планують так само позбавити магічності і число 34.
Насправді у фізиці офіційно є «магія», хоч це і магія чисел. Що у них магічного? Ми вважаємо, що ядра атомів складаються з позитивно заряджених протонів і нейтрально заряджених нейтронів. А всі ядра фізики умовно поділяють на стабільні і радіоактивні (нестабільні) за тим, як вони розпадаються. Поділ дійсно умовний, оскільки рано чи пізно кожне ядро розпадеться. Однак все ж вони роблять це з різною швидкістю і тому ті, що не встигли розпастися з часу утворення перших хімічних елементів, ми вважаємо стабільними. До чого тут магія? Фізики говорять, що така стабільність забезпечується певною кількістю протонів і нейтронів, які повністю заповнюють одну з оболонок ядра. До речі, якщо числа і протонів, і нейтронів магічні, то ядро називають двічі магічним і воно ще більш стабільне. Так до, наприклад, 2, 8 або 20, вчені з 2013 року намагалися додати число 32, яке помітили у надважких ізотопах кальцію - кальції-53 і кальції-54.
Однак, ще один експеримент з ЦЕРНу, «Ізольда» (ISOLDE), який займається дослідженням радіоактивних ізотопів, цього місяця поставив під сумнів «магічність» числа 32. Фізики вирішили перевірити сусіда кальцію за таблицею ізотопів, калій-51 і калій-52. Магічні числа знаходять за тим, як змінюються радіуси ядер, якщо до них додавати, наприклад, нейтрони. Так якби нейтрони ізотопів калію були магічними, то «підкинутий» нейтрон мав би збільшити радіус ядра, а вчені помітили б це за допомогою лазерної спектроскопії.
Втім, під час дослідження, з радіусом і калію-51, і калію-52 нічого не сталося, а тому жодних вказівок на «магічність» нейтронів з номером 32. Вчені стверджують, що так чином вони не спростовують результатів попередніх експериментів з кальцієм - вони дійсно могли вказати на число 32, однак навряд чи його можна назвати універсальним для всіх інших надважких ізотопів. Далі фізики з «Ізольди» планують перевірити ще одного кандидата на магічне число - 34, якого раніше знайшли у експериментах з кальцієм-53 та кальцієм-54.
Рекордна точність у вимірюванні ядра частинки
Цього разу вперше дані лазерної спектроскопії узгодилися з експериментами з розсіювання електронів, і фізики тепер у п’ять разів більш впевнені у розмірі радіуса ядра ізотопу гелію.
Будь-яку теорію необхідно перевіряти практикою, а зокрема вся фізика стоїть на тому, що нам вдається експериментально вимірювати константи з більш менш прийнятною похибкою як у рівняннях, так і у способах вимірювання. Втім, така зручна комунікація через формули іноді переходить у протистояння фізиків теоретиків та експериментаторів, коли останні знаходять нові способи вимірювати якісь величини. Одним із таких «полів бою» теорії та експерименту став радіус протона, який визначає не лише квантова електродинаміка, а і різні групи експериментаторів вже понад 10 років не можуть погодитися між собою. Так Комітет з даних для науки та технологій вважає, що радіус становить 0,877 фемтометра, але якщо пристосувати до вимірювання більш точний мюон, то радіус може бути 0,84 фемтометра і менше. Для нас це означає, що з експериментами все добре, вони і розходяться, підвищуючи точність, а от теорія сильно відстає - на 4-5 відсотків.
Отже, ми вже зрозуміли, що фізик-експериментатор обійде теоретика, якщо знайде спосіб виміряти щось ще більш точно. Приблизно з такими намірами і зібралася міжнародна група вчених та вирішила перевиміряти зарядовий радіус ядра ізотопу гелію. Про гелій ми знаємо, що його у космосі побачили значно раніше, ніж на Землі, що він другий за поширеністю після водню та має стабільне «магічне» ядро з двох протонів та двох нейтронів. Останнє є найцікавішим, адже так частинка є більш компактною, а парність складових її ядра спростить для вчених визначення спектру під час вимірювання. Тож ми беремо найпоширеніший з двох природних ізотопів гелію — гелій-4, зіштовхуємо за низького тиску з мюонами, а потім вимірюємо різницю між енергетичними рівнями, які вкажуть нам межі ядра гелію - його зарядовий радіус.
Так ми отримали радіус ядра гелію 1,67824 (83) фемтометра, що, на відміну від радіуса протона, збігається з попередніми експериментами, але є у п’ять разів точнішим. Це вперше результати лазерної спектроскопії узгоджуються з експериментами з розсіювання електронів. А у фізики з’явився спосіб пояснити структуру ядер через кварки і точно виміряти ядерні заряди елементів, важчих за гелій в експериментах зі значно меншими зусиллями без мюонних систем на великих прискорювачах частинок.
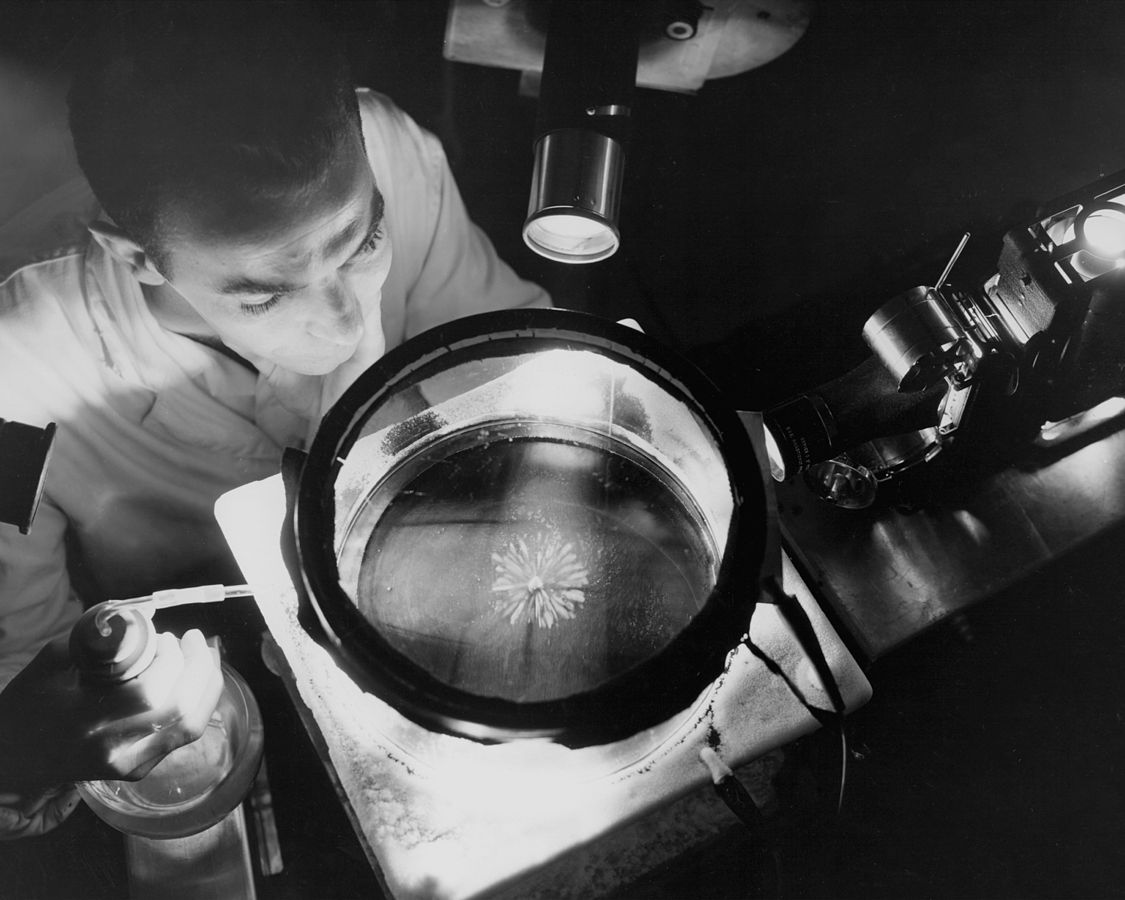
Фізик NASA вивчає альфа-промені у перенасиченій парі з туманної камери, де альфа-частинки з’являються у результаті розпаду полонію, 1957 рік. NASA/GRC/Bill Bowles
Максимальна швидкість квантових операцій
Вченим стало мало обмеження на кількість можливих операцій у двомірних квантових системах, тому тепер вони вирахували нове для більш складних. Новим параметром виявилася відстань, яку має пройти частинка - сума її проміжних станів.
Насправді обмеження, які постійно знаходять фізики не є чимось поганим, бо знаючи правила, легше навчитися грати, а особливо у фізику. У цьому є сенс, адже набагато легше передбачити те, чого не може статися, аніж намагатися прорахувати усі варіанти. А ще обмеження можна перейменувати у найбільш оптимальне рішення і так для квантових операцій, щоправда, лише дворівневих, з’явилося рівняння Мандельштама-Тамма. Радянські фізики прагнули знайти найкоротший шлях для частинки, за яким вона зможе «телепортуватися» з одного стану в інший. Так само працює брахістохрона Бернуллі, яка допомагає знайти найшвидший шлях перекотитися з точки А у точку Б. І так само радянські фізики вирахували тривалість найшвидшої можливої операції до того, як кубіт втратить свою когерентність.
Ми любимо квантові комп’ютери саме за вміння частинок одночасно знаходитися у стані «одиниці» або «нуля», а тому зберігати більше інформації, ніж звичайний біт — у них просто більше станів, відмінних від «чистих одиниць та нулів». Це все забезпечує явище суперпозиції, яке «змішує» для кубіта «одиницю» та «нуль». Однак, суперпозиція не може існувати вічно, а тому десь обов’язково з’явиться межа, за якою система втратить свою когерентність через взаємодію із зовнішнім світом. Для нас це означає повну втрату інформації та великі складнощі з тим, щоб змусити у системі працювати кілька частинок та зберігати більше таких «змішаних» станів. Так от для дворівневої системи, яку можна уявити як один кубіт, більш як 60 років тому знайшли формулу, за якою ми вирахуємо максимальний час її роботи. Це окремий випадок принципу невизначеності Гейзенберга — енергетична невизначеність, яка говорить, що поки частинка зберігає свободу вибору енергетичних станів, доти вона може існувати одночасно і в «нулі», і в «одиниці». Свої ступені свободи вона втрачає, взаємодіючи зі світом. Як і все, власне, у квантовій фізиці любить зникати за взаємодії із зовнішнім світом.
Але оскільки для квантових комп’ютерів дворівневої системи буде мало, варто було б знайти таку саму межу і для систем з більшою кількістю «змішаних» станів. Ми звичайно могли б підставити ту саму формулу Мандельштама-Тамма, однак тоді з’ясується, що мінімальний час замість того, щоб природно збільшуватися зі збільшенням відстані, починає зменшуватися. Тож цього разу, щоб врахувати всі компоненти та параметри, фізики вирішили внести також кількість проміжних станів, які матиме система. Так тепер, якщо ви раптом захочете створити квантовий процесор та максимально зменшити кількість помилок у ньому, фізики пропонують також врахувати, що саме відстань, яку проходитиме частинка, тобто число її проміжних станів, вплине з часом на перехід від керованого нами процесу до квантово-неконтрольованого.
Вчені визначили час утворення антиводню
Всього десять років тому ми навчилися «ловити» антиводень хоча б на 15 хвилин, щоб дізнатися про антиматерію трошки більше, окрім того, що вона анігілює з матерією. Один з експериментів займається пошуком «антигравітації» і цього місяця вони стали на крок ближчими, вирахувавши час народження античастинки.
Як можна було помітити з попередніх новин, фізикам дуже подобається шукати симетрію та порушувати її. Головною для всіх фізичних явищ, які ми спостерігаємо, та законів, які їх описують, вчені вважають СРТ-симетрію. Вона говорить нам, що «дзеркальне зображення» нашого Всесвіту має еволюціонувати за тими самими фізичними законами, що діють і для нас, навіть якщо змінити напрямок плину часу, орієнтацію просторових осей та зарядів усіх складових системи. Втім, нас з вами тут би не було, якби одного разу симетрія зарядів та простору, яка перетворює матерію на антиматерію, не порушилася би та першої виявилося більше. Без порушення симетрії, матерії мали б анігілювати, але нам пощастило. І тут знову варто повернутися до проблеми теорії та практики — все це нам потрібно якось перевірити. Так у 1995 році фізики з ЦЕРНу оголосили, що вони створили перші атоми антиводню на Антипротонному кільці з низькою енергією (LEAR).
У тому експерименті атоми були занадто «гарячими», а тому їх було важко втримати для дослідження. Але вже у 2011 у тому ж ЦЕРН вчені з експерименту ALPHA змогли впіймати антиводень у пастку більш як на 16 хвилин. Звичайно знайти і навіть втримати атоми антиводню є великим проривом для фізики, однак шукали ж ми його, щоб подивитися, чи діють на нього такі самі закони, як і на звичайний водень. Тож потім з’явилося два нових експерименти, які прагнуть перевірити, чи існуватиме якась антигравітація абощо для античастинки. Один з них, AEGIS, шукає прискорення вільного падіння (та сама g з формули для сили тяжіння). І цього місяця вчені з AEGIS представили нові результати експериментів, які можуть наблизити нас до розуміння того, що ж відбувається з антиводнем, окрім того, що він анігілює з матерією.
Антиводень утворюють з позитрона та антипротона, який народжується на антипротонному сповільнювачі. По суті протони змушують стикатися з металевою мішенню, а вже у зіткненні ми зможемо впіймати антипротон. Втім, не всі вони підходять, а тому найшвидших відпускають, а от атоми з меншою енергією лишаються у пастці. Ми не можемо експериментально спостерігати момент утворення антиводню, однак ми знаємо, скільки часу потрібно позитрону, що дійти до антипротона та утворити антиводень. Схема, за словами дослідників, дає змогу визначити час утворення 90 відсотків атомів з похибкою близько 100 наносекунд.
На квантовому комп’ютері змоделювали фрустрований магніт. Це квантова перевага
Інженери з D-Wave досягли квантової переваги, навчивши свій обчислювач моделювати поведінку спінів у фрустрованому магніті. Класичному комп’ютеру на цю задачу знадобилося б занадто багато часу.
Поняття квантової переваги взагалі дуже умовне і ніхто точно не формулював, що має зробити квантовий комп’ютер, щоб ми в один момент викинули свої кремнієві чіпи. Проте загалом ми можемо окреслити межу — квантовий процесор має за оптимальний час розв’язати задачу, на яку класичному знадобилися б роки. Цього разу квантовий комп’ютер D-Wave мав справитися із реальною фізичною задачею — змоделювати поведінку фрустрованих магнітів. За словами дослідників, рішення такої прикладної задачі, яка необхідна для дослідження топологічних явищ, спінових рідин та магнітних фазових переходів у квантових системах, репрезентує квантовий комп’ютер як реальний додаток для реальних експериментів. Про використання квантових процесорів для фізичних прикладних задач заповідав ще Фейнман.
Предметом моделювання став фрустрований магніт. Фізика розглядає магніти як певне розташування спінів частинок, які можуть розміститися так, що сумарний магнітний момент відрізняється від нуля і з’являються магнітні властивості. Фрустрованим магніт ми називаємо, якщо він через геометрію не може впорядкувати свої спіни: побудуйте з атомів ромбоподібну сітку і форма трикутників просто не зможе дозволити спінам вишикуватися впорядковано. Так вони не впорядковуються навіть за низьких температур, продовжують колективно рухатися і таким чином переносити, наприклад, тепло. Обчислювачу D-Wave вдалося прослідкувати час встановлення рівноваги у досліджуваній ними решітці та побачили чергування «порядку з безладом», яке призвело до втрати магнітних властивостей.
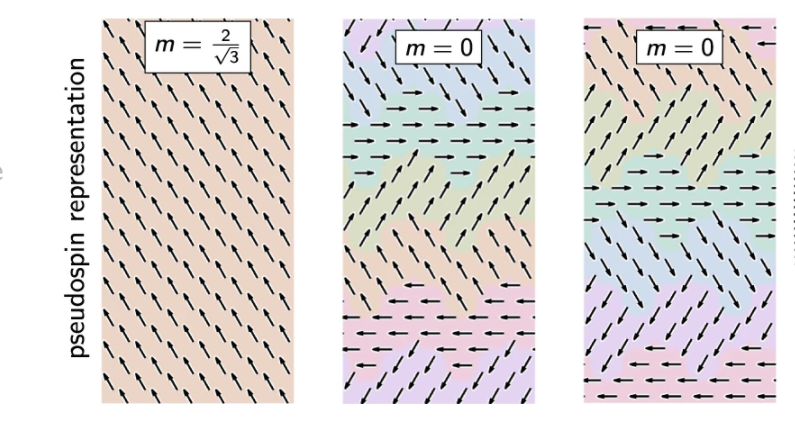
Моделювання поведінки спінів у впорядкованому стані та обертаючись за або проти годинникової стрілки, чергуючи «порядок з безладом». Andrew D. King et al. Nature Communications, 2021
З чим розібрався D-Wave? Перед комп’ютером поставили задачу, за яку у 2016 році вручили Нобелівську премію з фізики — дослідити топологічні фазові переходи у магнітах, які виникають у результаті конкуренції між квантовими і тепловими флуктуаціями. D-Wave — канадські розробники, які вирішили йти дещо інакшим шляхом та будувати окремо квантові обчислювачі для конкретних задач, а не цілий комп’ютер. За словами компанії, успішна демонстрація таких складних явищ сама по собі є ще одним доказом програмованості та обчислювальної гнучкості квантового комп'ютера D-Wave. Головною перевагою свого дослідження вони вважають, що комп’ютер справився не з синтетичною, спеціально придуманою квантовою задачею, а з реальною фізикою, що вказує на можливість використання квантових обчислювачів як звичайного інструменту для моделювання.
Квантовий обчислювач обігнав класичний у розв’язанні задачі. Це також квантова перевага
Квантовий комп’ютер хоч і не розв’язав одну з семи задач тисячоліття, однак зміг обійти класичний у перевірці рішення однієї з задач NP класу, на яку останньому знадобилося б у тисячу разів більше бітів.
Як ми вже вказали, квантова перевага — поняття відносне, а перевірка результату, його валідація, можлива лише для дуже вузького діапазону параметрів, які іноді просто недоступні класичним комп’ютерам (а часто і не потрібні). Поки більшість задач, розв’язаних квантовим комп’ютером просто не мають прикладної цінності та просто демонструють можливості технології. Такі задачі ми ділимо на ті, для яких є «швидкі» алгоритми розв’язання (P клас), та ті, лише розв’язок яких ми можемо знайти за поліномінальний час (NP клас). Однак, центральною проблемою математики, одна з семи задач з тисячоліття, є рівність цих класів задач. Адже якщо ми можемо швидко перевірити якийсь розв’язок, то чи могли б ми так само швидко його знайти?
Задачі NP класу ми можемо звести до алгоритмічної задачі здійсненності булевих формул, де ми намагаємося призначити всім змінним, які є у формулі, значення хибності або істини, щоб формула стала істинною. У своїй роботі фізики експериментально продемонстрували, як квантовий обчислювач, маючи у тисячу разів менше біт, ніж класичний, владнав з перевіркою рішення NP-повної задачі. Для цього йому знадобився квантовий Мерлін і Артур, які обмінювалися рішенням та перевіркою задачі за допомогою детектування поодиноких фотонів та їхніх когерентних станів. Для того, щоб покращити результати роботи комп’ютера, вчені збільшували «бажання» Мерліна помилятися навіть якщо він отримає правильний розв’язок, та при цьому обмежували його під позитивної оцінки помилкового результату.
За словами дослідників, їхній результат наближує квантові обчислювачі до реального застосування, тим паче що вони використовували просте обладнання, доступне у лабораторіях квантової фотоніки, а також їхній результат є не розподілом імовірності рішень, а цілком піддається перевірці, оскільки на виході виходить відповідь «так» або «ні».











