Американські математики проаналізували заміряний секундомірами час, за який спортсмени пропливали дистанцію у басейні, та дійшли висновку, що алгоритми годинника допускають похибку навіть у 0,09 секунди. Це проблема помилки чисел із рухомою комою, яка у 647 запливах призвела до значної похибки внаслідок округлення. Занепокоєністю щодо оцінки часу під час спортивних змагань та у фізичних експериментах вчені поділилися у American Journal of Physics.
Що рахували математики?
Час є невідновним ресурсом, який ми всі постійно рахуємо. А для спортсменів тим паче не існує поняття «плюс-мінус п'ять хвилин» — їм надзвичайно важливий точний час. Головною складовою будь-якого вимірювального пристрою є осцилятор — предмет, який коливається з певною частотою (чим менше вона відхиляється від заданого значення, тим точніше годинник). Сучасні годинники, а зокрема і секундоміри для спортсменів, працюють на кварцевих кристалах. Кварц є ідеальним резонатором, який коливається із чітко визначеною частотою і тим самим забезпечує виключну точність.
Так годинники вимірюють час, рахуючи передбачувані коливання кварцового кристала. А остаточний рахунок перетвориться на звичні нам секунди з десятковими знаками в форматі числа з рухомою комою. У своїй роботі математики Девід Фаукс і Джанет Годолфін (David A. Faux and Janet Godolphin) вивчили доступний їм обсяг даних про перегони, щоб спробувати знайти систематичну помилку округлення та викрити секундоміри у неточності. За розрахунками вчені звернулися до плавання — ідеального, на їхню думку, спорту для збору великих обсягів даних, бо одне тригодинне змагання зазвичай дає 300-400 результатів, які можна отримати у відкритому доступі. Тож дослідники зібрали результати 647 запливів з секундоміром та спробували проаналізувати частоту появи відображуваних конкретних цифр на секундомірах суддів.
Що вдалося наміряти?
Фаукс і Годолфін зосередилися на двох останніх відображуваних цифрах (десята і сота секунди) та подивилися, чи є якісь «популярніші» значення, порівняно з іншими. Типовий час запливу на дистанції до 100 метрів коливається від 28 до 120 секунд, залежно від виду змагання і віку учасників. Так вчені отримали набір з 3 014 615 змодельованих годин, де в середньому кожна пара цифр повинна з'являтися з ймовірністю 1 відсоток. Результати їх вразили: три пари цифр, а саме 00, 50 і 75, складають більше однієї восьмої результатів. Причому разом із тим є вісім пар цифр, які жодного разу не траплялися на секундомірах.
Вчені додатково оцінили свої результати за критерієм узгодженості Пірсона, що дає змогу оцінити статистичну значущість відмінностей двох або більше відносних показників. Так за гіпотези, що кожна сота на секундомірі матиме однаковий шанс опинитися на дисплеї, очікуване значення критерію складає 99, а те, що перевищуватиме 125, буде вказувати на те, що дані значно відхиляються від гіпотези про рівність виміряних хронометристом значень. Однак тест показав значення 740, що приблизно на 45 стандартних відхилень перевищує очікуване значення та вказує на статистичну неможливість того, що кожна сота, виміряна секундоміром, має рівну імовірність. Деякі пари десятих і сотих з'являлися всього 6873 рази, тоді як інші зустрічалися всі 81606 разів.
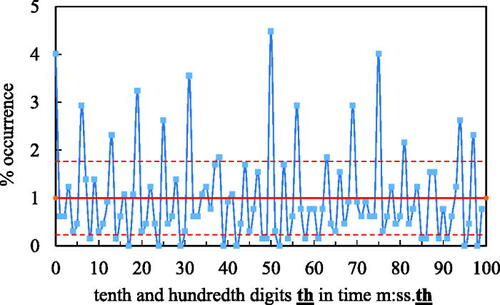
Відсоток появи двох останніх відображуваних цифр на дисплеях секундомірів, що використовувалися на двох змаганнях з плавання. Очікуване середнє значення в 1 відсоток та стандартне відхилення позначене горизонтальними суцільними червоними лініями і червоними пунктирними лініями відповідно. Спостережуваний розподіл статистично неможливий, якщо кожна сота має однакову імовірність появи на екрані. David A. Faux and Janet Godolphin / American Journal of Physics, 2021
Звідки взялася помилка?
Річ не в тім, що годинник може неправильно взаємодіяти із кварцевим кристалом, або сам кристал раптом змінив періодичність своїх коливань. Хоча пристрої точно реєструють час всередині, як механізм, вони роблять помилки при перетворенні необроблених даних в значення, легких для читання людиною. Числа, після приведення їх до десяткового виду, містять як правильні цифри, так і «хвости» з неправильних. Ці «хвости» і є джерелом помилкових обчислень десяткових дійсних. Число з рухомою комою саме по собі є точним, але для обмеженого дисплеєм пристрою його може виявитися забагато. Перш за все, ці помилки округлення відбуваються через те, що нескінченність всіх дійсних чисел неможливо представити в умовах обмеженості пам'яті пристроїв, тож отримувані нами на дисплеях числа є лише наближеннями до реальних значень.
Так математики дійшли висновку, що це спричиняє помилки округлення. Причому комп'ютерна модель секундоміра із трьома мільйонами симуляцій не вказала на подібну помилку, але тільки-но значення у ній перевиміряли за допомогою алгоритму, аналогічного тим, які використовуються для відображення чисел в секундомірах, вчені знову побачили спотворений розподіл значень. Фаукс і Годолфін вважають, що така проблема може торкнутися широкого спектра пристроїв від безлічі виробників, адже алгоритм перетворення використовуваних чисел з рухомою комою є галузевим стандартом — IEEE 754. Математики бачать рішення проблеми у зміні таблиць переформатування отриманих значень, щоб алгоритми могли краще перетворювати кількість коливань кварцевого кристала у відповідний час в секундах.
То вчені пропонують анулювати результати олімпіад?
За їхніми словами, отриманий за допомогою секундомірів час, чи то у спорті, чи то у результаті лабораторних фізичних експериментів, має помилку округлення, аналогічну за величиною до невизначеності, пов'язаної із реакцією людини. Не важливо, як точно ви можете натиснути «старт» і «стоп», якщо секундомір вже вирішив все за вас. У статті вчені згадують суперечливий заплив на 100 метрів батерфляєм на Олімпійських іграх 2008 року в Пекіні. Тоді перемогу отримав Майкл Фелпс, обійшовши свого суперника Милорада Чавича всього на 0,01 секунди. «Ми підкреслюємо, що у нас немає доказів того, що подібні часові аномалії мали місце у тих змаганнях. А також ми не впевнені навіть що вони існують в електронних системах хронометражу, використовуваних на спортивних змаганнях високого рівня, де помилка округлення може бути виправлена» — зазначають дослідники у своїй статті.
Втім, затим вони надають результати із перегонів двох плавців — «А» та «Б». Так за час запливу першого відбулося 1660659 кварцових коливань, а отже «правдивий» час — 50.6800 секунди. У другого коливань відбулося 1657710, тож правильний час — 50.5900. Але секундоміри вирішили інакше та віддали перемогу плавцю «А», порахувавши його час як 50.57 секунди проти 50.58 плавця «Б». Це наочний приклад того, як через помилку округлення перевагу отримав спортсмен, який прийшов насправді другим, тому необхідно знайти спосіб виправити ці помилки алгоритму, визнаючи всі ризики.
