Вчені пристосували неможливість обійти швидкість світла до криптографії та реалізували протокол передавання даних із NP-повною задачею з розфарбування вершин графа у три кольори між двома пристроями. Метод спрацював як на відстані у 400 метрів між парою того, хто доводить і того, хто перевіряє ключ, так і на менші відстані у 60 метрів. Деталі експериментів дослідники опублікували у Nature та пропонують використовувати свій принцип для усіх методів шифрування, які покладаються на NP-повні задачі.
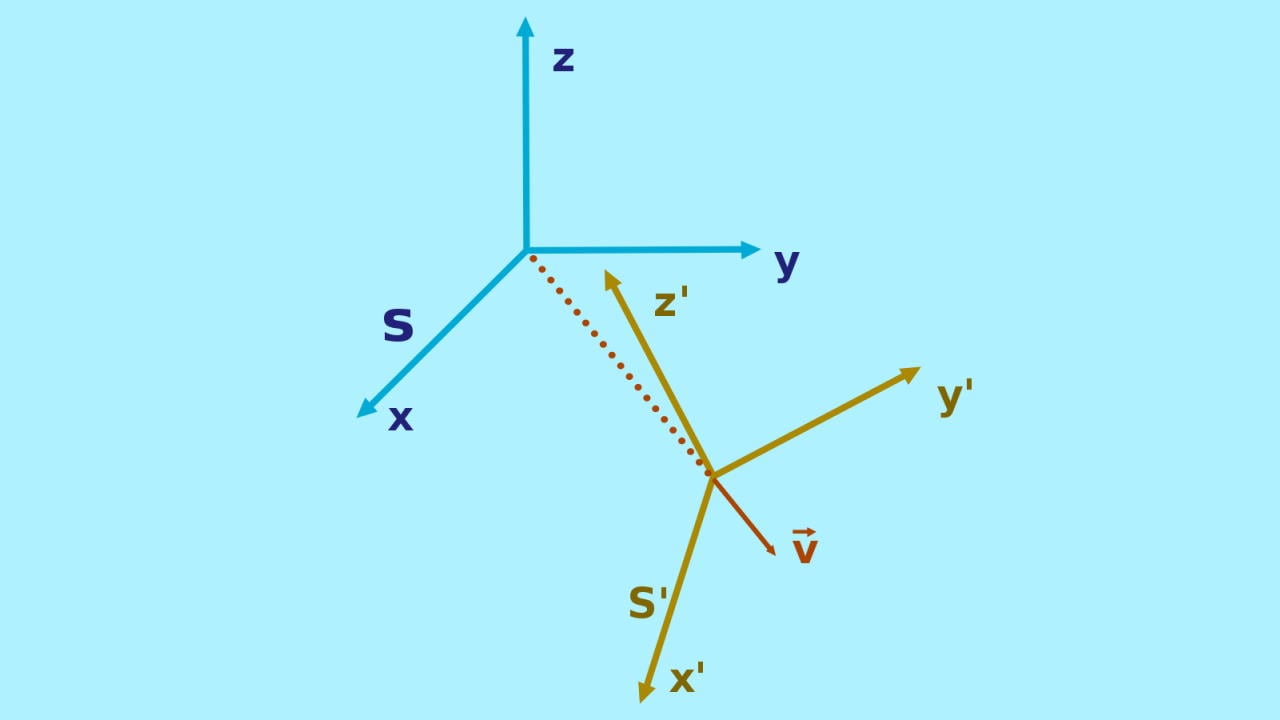
З огляду на принцип відносності, швидкість світла у вакуумі c однакова у будь-якій системі відліку. Brews ohare / Wikimedia Commons
Яку задачу потрібно розв'язати?
Складність будь-якої задачі, для якої існує алгоритмічне рішення, оцінюється з урахуванням часу, який знадобиться на її розв'язання або, навпаки, на перевірку цього розв'язку. Відповідно P клас задач об'єднує задачі, для яких час розв'язання поліноміально залежить від розміру вхідних даних, а NP — клас складності задач, розв'язання яких можна перевірити за поліноміальний час за наявності додаткових відомостей. Власне, пошук «найшвидшого» алгоритму криється у доведенні чи спростуванні рівності між собою цих двох класів.
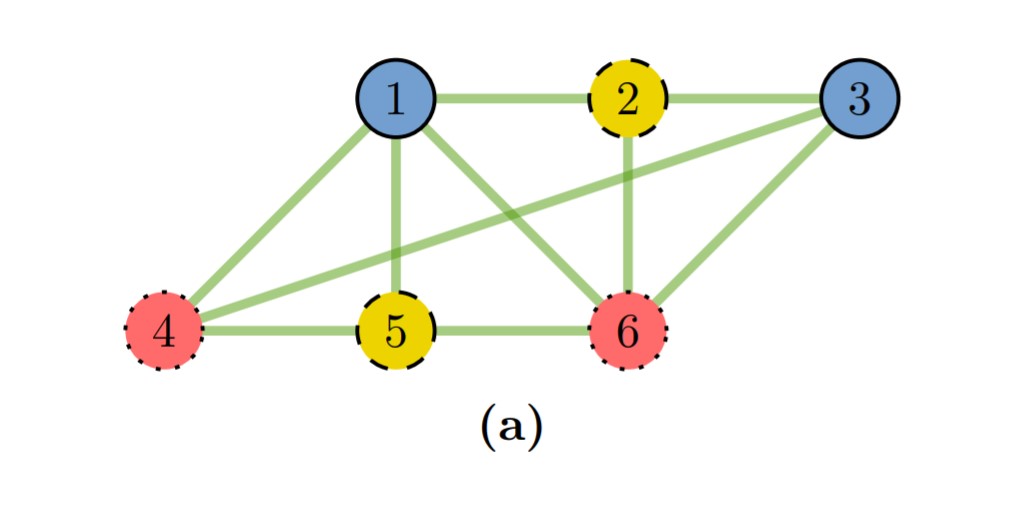
У класі NP також виділяють такі завдання, до розв'язання яких можна поліноміально підвести і пошук розв'язків будь-якого іншого завдання класу NP. Тоді їх називають NP-повними задачами. У цій роботі науковці з Канади, Швейцарії і Китаю розглянули одну з таких задач – розфарбовування графа у три кольори. Вона вимагає розфарбувати вершини графа у три кольори так, щоб будь-які дві вершини, які мають спільне ребро, мали різні кольори. Деякі графи можуть бути триколірними, деякі — ні, і загальна проблема визначення того, чи є граф триколірним, немає відомого ефективного рішення. Проте перевірити, чи різного кольору вершини графа можливо, а тому задача належить до тих, які можна ефективно перевірити за наявності рішення.
До чого тут криптографія?
У вступі до своєї роботи автори пропонують уявити таку ситуацію: у чужому місті ви шукаєте банкомат, щоб зняти кошти місцевою валютою зі своєї банківської картки. Вам трапляється банкомат невідомого банку, який, звичайно, просить вас ввести ваш PIN-код для отримання грошей. І ви його надаєте — свою конфіденційну інформацію — щоб отримати кошти. Але чи можна довіряти невідомому банку? У вас нема жодних вагомих причин на це. Власне, як і у банку нема причин вам довіряти, окрім як через отриманий PIN-код, який дасть змогу припустити, що ви і є власником коштів. І дослідники спробували знайти новий спосіб довести, чи є дійсно хтось власником картки, не видаючи при цьому такі дані.
Вперше подібними питаннями задалися ще у середині 1980-х років — так з'явилася ідея доведення з нульовим розголошенням. Дуже коротко суть цієї задачі полягає у тому, як би вам переконати когось у тому, що ви можете довести твердження, але при цьому не розкрити саму відповідь або процес доведення. Так у вас є дві сторони: та, що перевіряє (її зазвичай називають Віктором від англійського «The verifier») і та, що доводить (її зазвичай називають Пеггі «The prover»). Причому протокол має враховувати, що той, хто доводить, зможе переконати того, хто перевіряє, лише у тому випадку, якщо його твердження справді правильне.
Найбільш поширеним її варіантом є завдання ідентифікації, коли користувач може підтвердити свою особу, знаючи секретний доказ твердження, яке він створив та опублікував. Зараз задачу використовують банки і блокчейни криптовалют, і ви, імовірно, також стикалися з нею, якщо користувалися сервісами, які працюють з алгоритмом RSA, в якому математичним секретом є факторизація ще більшого числа на два величезні прості числа.
До чого тут спеціальна теорія відносності?
Хоч формулювання доведення з нульовим розголошенням із задачею з розмалювання графів з'явилося майже одразу — у 1991 році, воно автоматично сформулювало необхідність у цих додаткових даних для ідентифікації — ключах. А отже доведення з нульовим розголошенням для будь-якої NP-повної задачі, такої як і трикольорове розфарбування графів, неможливе без додаткового обчислювального припущення. В іншому випадку це довело б нерівність класів NP і P, а з цим і нашу впевненість у існуванні «найефективнішого алгоритму».
Втім, існує й обхідна концепція, яка пропонує замість додаткових даних використовувати кількох Пеггі, які б доводили одному Віктору своє твердження. Інтуїтивно цей підхід відображає стратегію, яку використовують слідчі поліції при допиті підозрюваних. Колективно збрехати набагато складніше, ніж при роздільному допиті.
Ключова різниця між сценарієм з декількома сторонами, що доводять, та використанням додаткового секретного доказу полягає у тому, що необхідно знайти спосіб заборонити різним Пеггі спілкуватися між собою. Це, звісно, передбачає якесь просторове розділення Пеггі. І тут вченим і стала в пригоді спеціальна теорія відносності, яка постулює — ніщо і ніхто не може спілкуватися швидше за швидкість світла.
Як СТВ захистить обмін даними?
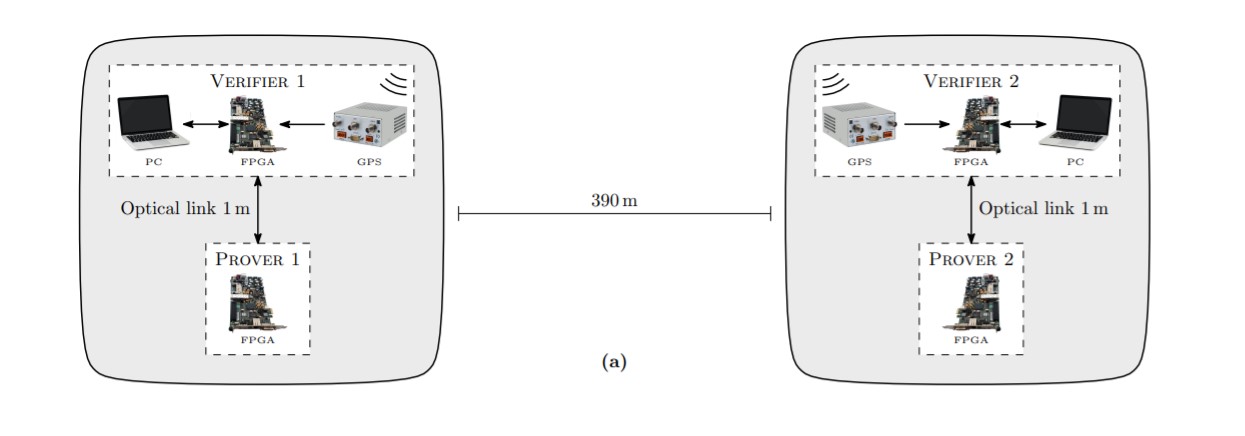
Виходячи з принципу спеціальної теорії відносності, існує коротке часове вікно, протягом якого Пеггі фізично не можуть передавати один одному сигнали. І в цій роботі цю ідею вдалося експериментально реалізувати для двох розділених пар Пеггі-Віктор. У першому експерименті дві пари розміщуються у різних будинках на території кампуса на відстані 390 метрів один від одного, що відповідає часовому поділу 1,3 мікросекунди. Обидва Віктори надсилають своїм сусіднім Пеггі потік запитів. Загальний час, що минув між передаванням запитів перевіряючих та отриманням відповідей, становить 840 наносекунд, що менше встановленого часового інтервалу між сторонами та забезпечує надійність.
Проте, в успіху свого протоколу на великих відстанях вчені не сумнівалися. І тому у другому експерименті пари посадили за двома столами (по парі на кожний) на відстані 60 метрів один від одного, що відповідає часовому поділу 200 наносекунд. Між двома верифікаторами передається сигнал. Коли вони ним обмінюються, другий відправляє запит стороні, що доводить, до якої він підключений. У цей час перший затримує відправлення свого запиту на час, необхідний для обміну запитом другому. Таким чином, обидва верифікатори надсилають своїм «пруверам» потік запитів. Загалом раунд досягається максимум за 192 наносекунди, що обмежує мінімальну відстань, можливу для реалізації ідеї, на 57,6 метра.
Важливо відзначити, що безпека забезпечується релятивістськими обмеженнями і не покладається на обчислювальні гіпотези, такі як існування односторонніх функцій. А вищезгадана NP-повнота задачі гарантує, що будь-який застосунок, заснований на задачах класу NP, може бути (поліноміально) перетворений на екземпляр створеного протоколу. Наприклад, якщо ви довіряєте Advanced Encryption Standard (AES) як безпечному криптографічному примітиву, можна перетворити екземпляри AES на графи з вершинами трьох кольорів.
Оновлено 12.11 о 10:06: У другому експерименті, так само як і в першому, йшлося про дві пари сторін, що перевіряють, і що доводять. Ми вказали, що їх розмістили попарно за одним столом на відстані 60 метрів, втім, столів було два, за кожним з яких була пара. А також некоректне «програма» замінили на кращий варіант - «застосунок».