Американські фізики надрукували п'ять різних форм, що мали характеристики ізотропних гелікоїдів, та пустили їх поплавати у силіконовій олії. Ті мали почати обертатися, відповідно до 150-річної теорії математика лорда Кельвіна. Однак, не зважаючи на це, потрібної поведінки вчені не помітили, про що повідомили у журналі Physical Review Fluids.
Що за ізотропний гелікоїд?
Гелікоїди належать до мінімальних поверхонь з нульовою середньою кривизною. Загалом це гвинтоподібна форма, яку описують прямою, яка обертається з постійною кутовою швидкістю навколо нерухомої осі. Вона перетинає вісь руху під постійним кутом і одночасно переміщується поступально з постійною швидкістю вздовж цієї осі. Причому швидкості цих рухів пропорційні. Гелікоїд став частиною красивої теоретичної ідеї про те, що така спіральна частинка може поводитися як ізотропна та відчувати однаковий тиск рідини з усіх боків, при цьому обертаючись у ній. Ідея з'явилася 150 років тому, але останнім часом такі хіральні взаємодії у турбулентних рідинах стали областю активних досліджень. На додачу розвиток 3D-друку дав змогу фізикам перевірити, чи здатний гелікоїд відчувати такий же поступальний опір в однорідному потоці рідини при будь-якій орієнтації, як і звичайна сфера. Загалом це неможливо, адже на відміну від сфери, на ізотропний гелікоїд діє крутний момент, коли він рухається через рідину. А для збереження ізотропності, цей крутний момент повинен бути незалежним від орієнтації частинок щодо потоку, що виключає спіральність. Втім, лорд Кельвін, автор теорії, припустив, що якщо створити спіральну частку, розмістивши 12 лопатей навколо великих кіл сфери, то рідина дійсно може надавати нерівномірний тиск і розкручувати гелікоїд. Але поки опублікованих експериментальних вимірювань ізотропних гелікоїдів немає, виправленням чого і зайнялися дослідники Весліанського університету.
Як фігура повела себе в експерименті?
У своїй роботі за допомогою стереолітографічного 3D-друку виготовили п'ять різних форм ізотропних гелікоїдів лорда Кельвіна. Для лопатей використовували сегменти сфероїдальних дисків діаметром 8,7 міліметра, а згідно із пропозицією вченого, центри дисків рівномірно розподілили навколо трьох великих кіл твердої сфери з кутом нахилу 45 градусів. Діаметр першої експериментальної кулі складав 17,4 міліметра — її фізики кинули у силіконову олію з щільністю 0,98 грама на кубічний сантиметр, де гелікоїд осідав зі швидкістю 4,74 сантиметра на секунду і жодного разу не покрутився — його найкраща кутова швидкість склала мінус 0,003 радіана на секунду. Швидкість обертання вдвічі перевищує випадкову похибку вимірювання, а систематичні похибки, пов'язані з виробничими дефектами, які змушують частинку обертатися навколо інших осей зі швидкістю, аналогічною виміряному обертанню, вчені оцінили в один відсоток. Тобто гелікоїд все ж зовсім не обертався. В інших варіантах частинки також не помітили обертання в межах похибки вимірювання, а тому вчені доходять висновку, що будь-який гелікоїд, зроблений з невзаємодіючих нехіральних лопаток, повинен мати нульове середнє обертання.
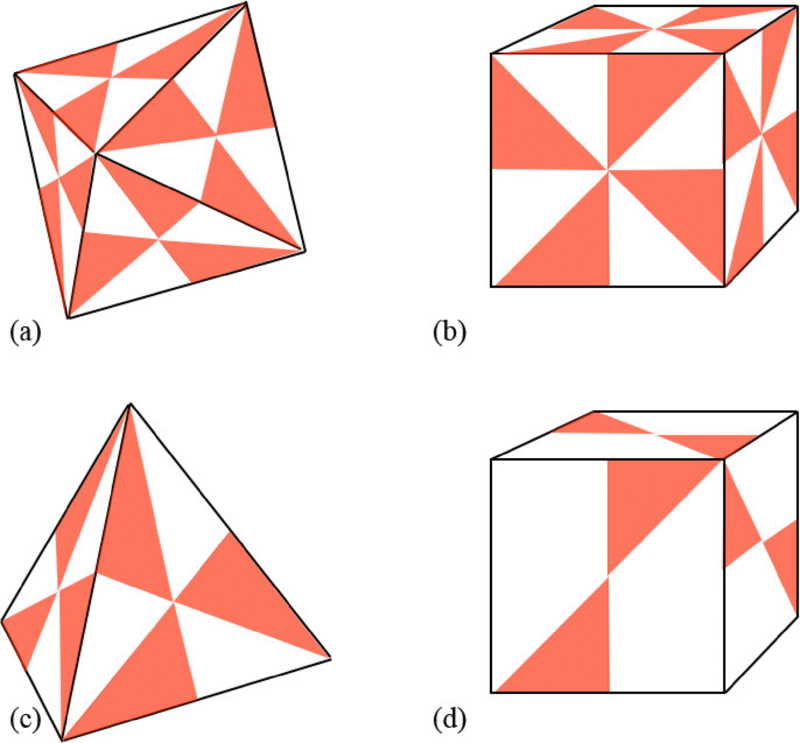
Малюнок ілюструє точкові симетрії різних ізотропних гелікоїдів. Darci Collins et al. / Physical Review Fluids, 2021
Чому гелікоїд не закрутився?
Є принаймні два можливих пояснення цій розбіжності теорії та експерименту. По-перше, проблема твердого тіла, що осідає в рідині, може мати іншу симетрію, яка призводить до зникнення поступально-обертального зв'язку, незважаючи на те, що це допускається симетрією геометрії частинки. По-друге, зв'язок обертання і поступального руху для цих частинок може бути ненульовим, але просто занадто слабким, щоб його можна було надійно виявити в експерименті. Свої результати вчені пояснювали з точки зору симетрії, яка призводить до зникнення обертально-поступального руху ізотропного гелікоїда. Чисельні значення підтверджують, що ця ізотропна частинка демонструє невеликий, але ненульовий зв'язок обертально-поступального руху в межі повзучого потоку рідини, що узгоджується з аналізом симетрії, але ефект занадто малий, щоб його можна було побачити в експериментах. Можливо, «правильний» кельвінівський гелікоїд й існує, але його форма має бути набагато складнішою, тому у вчених ще є поле для майбутніх експериментів.







