Вчені розробили новий метод математичного аналізу, який дає змогу систематично характеризувати біологічні системи, здатні до самоорганізації без центрального елемента. Ця робота зосереджена на реакційно-дифузійних системах, моделях, які описують, як хімічні частинки змінюються в просторі і часі, де загальна кількість цих частинок залишається постійною і пояснює таку поведінку наявністю нульових ліній, вздовж яких одна з двох змінних системи знаходиться в рівновазі. Результати роботи вчені описали у статті, опублікованій у журналі Physical Review X.
Навіщо математикам біологічні системи?
Багато процесів, що відбуваються в біологічних клітинах, залежать від утворення молекулярних структур, які здатні самоорганізовуватися. Наприклад, певний просторовий розподіл визначених білків регулює поділ клітин, їхню міграцію і ріст. Ці закономірності є результатом узгодженої взаємодії багатьох окремих макромолекул. Подібно самоорганізації пташиних зграй, цим процесам не потрібен центральний координатор. Досі математичне моделювання формування патерну поведінки білків у клітинах виконувалося в основному за допомогою складних комп'ютерних симуляцій, які були зосереджені на динаміці цих білків в однорідних стійких, тобто лінійних, станах. А робота над повністю розвиненими патернами у нелінійних станах обмежувалася лише числовими дослідженнями, які було складно провести через велику кількість вхідних даних. Нова робота математиків є новим методом, який забезпечує систематичний математичний аналіз процесів формування таких патернів самоорганізації біологічних систем.
Дослідження зосереджено системах, які зберігають центр маси, тобто в яких взаємодії впливають на стан присутніх в системі частинок, але не змінюють їхню загальну кількість. Ця умова виконується в системах, де білки можуть перемикатися між різними конформаційними станами, які дають змогу їм, наприклад, зв'язуватися з клітинною мембраною або утворювати різні багатокомпонентні комплекси. Через складність динаміки в цих системах, формування таких структур досі вивчається за допомогою трудомісткого чисельного моделювання, однак тепер, за словами вчених, можна зрозуміти основні особливості формування патернів незалежно від моделювання, використовуючи прості обчислення і геометричні конструкції. Ця теорія забезпечує міст між математичними моделями і колективною поведінкою компонентів різних біологічних систем: геометричний опис дає змогу зрозуміти, чому виникають різні моделі поведінки, що визначає їхню взаємодію та чи можна ці принципи поширити на всі системи, здатні самоорганізовуватися.
Що з’ясували вчені?
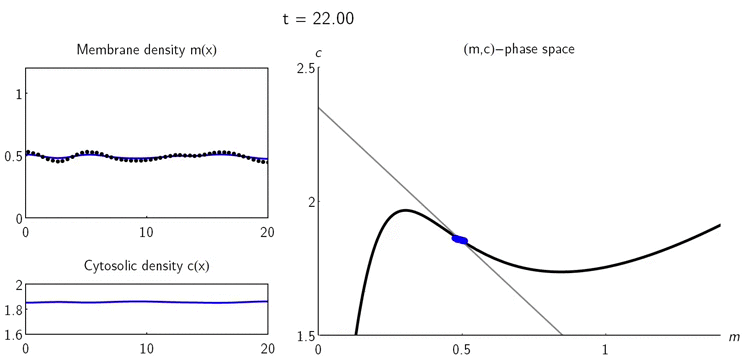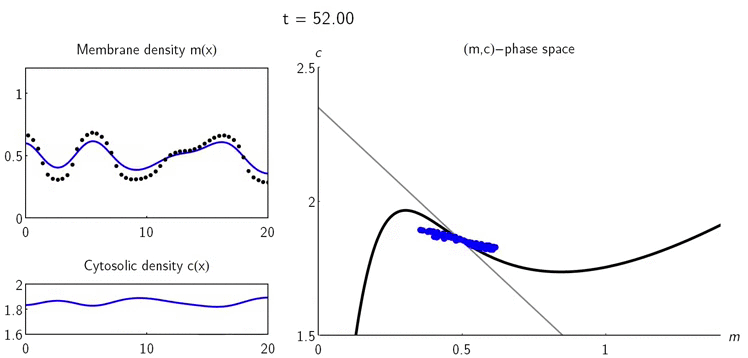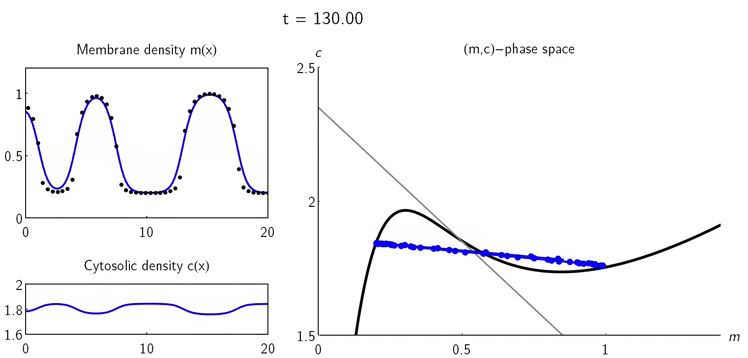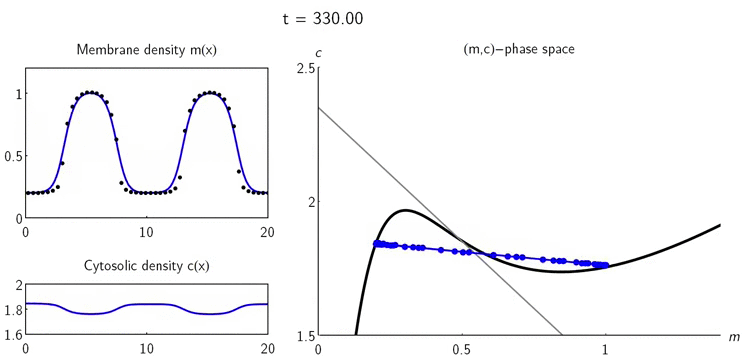
Ця робота зосереджена на реакційно-дифузійних системах, моделях, які описують, як хімічні елементи змінюються в просторі і часі, де загальна кількість цих елементів залишається постійною. Ключовий висновок полягає в тому, що зміни в локальних точках щільності зрушують точки реактивної рівноваги, що спричинює утворення градієнтів концентрації, які і є причиною перерозподілу частинок. Математики описали цю взаємодію простими геометричними об'єктами в фазовому просторі та ввели теорію локальної рівноваги частинок, яка дає змогу аналізувати і характеризувати як початкове зростання системи, так і можливу стабілізацію патернів поведінки. В рамках цієї структури багато властивостей нелінійної динаміки реакційно-дифузійних систем зі збереженням маси тепер можуть бути безпосередньо розглянуті в термінах геометрії, що в іншому випадку було доступним лише чисельному аналізу. Фундаментальні елементи їхньої теорії можна узагальнити на широкий клас подібних нерівноважних систем.
Як вони дійшли своїх висновків?
Спроби пояснити здатність біологічних систем до самоорганізації за допомогою геометрії були ще у минулому столітті у роботах Анрі Пуанкаре. У своїй роботі вчені використали як геометричні об’єкти нульові лінії - геометричне місце поєднання точок поперечного перерізу з нульовими нормальними напруженнями, тобто мірою інтенсивності внутрішніх сил. Їх математики визначили як криві фазового простору, вздовж яких одна з двох змінних системи знаходиться в рівновазі. Одним з ключових переваг такого геометричного підходу до нелінійних динамічних систем є те, що він дає систематичне фізичне розуміння процесів, які керують динамікою, не вимагаючи рішення окремих рівнянь.
Аналіз фазового простору двокомпонентних систем показав, що просторові варіації щільності білка призводять до просторово неоднорідних локальних рівноваг. Співвідношення між масою і реактивною рівновагою геометрично представлена як реактивний нульовий кут, уздовж якого кінетика залишається врівноваженою. Цей кут є центральним геометричним об'єктом, який організовує просторово-часову динаміку частинок. Тобто патерни локальних рівноваг, які ведуть до самоорганізації системи, “кодуються” положенням цих ліній. Нахил нульової лінії забезпечує параметр для виникнення нестабільності, яка запускає перерозподіл мас і патерн організації системи.